Chemistry Graphics- by Topic •Basics (elements & measures) •Atomic Structure •Periodic Properties •Nuclear •Moles •Stoichiometry •Gases •Bonding •Phase Change •Colligative Properties •Thermodynamics •Equilibrium •Kinetics •Acid-Base •Electrochemistry •Molecular Structure/Geometry •Complex Ions Physics •Physics Graphics •Physics Videos Biology •Biology Graphics •Biology Videos•Forensics Graphics Chemistry Videos- by Topic •The Basics •Physical & Chemical Properties •Atomic Structure Pt.1 •Nuclear •Moles, Molarity, Reaction Types •Stoichiometry •Gas Laws •Atomic Structure - Part 2 •Bonding & Geometry •Intermolecular Forces •Thermochemistry •Colligative Properties •Thermodynamics •Gas Phase, Solubility, Complex Ion Equil. •Kinetics •Acid-Base Equilibria •Electrochemistry •Miscellaneous Mathematics ——Graphics  -  by Subject—— •Algebra •Statistics •Precalculus / Trig •Calculus ——Videos  -  by Subject—— •AP Calculus Music Instruction Videos - by Topic •Where Music Meets Science •Linear Theory •Vertical Theory •Advanced Music Theory •Piano Instruction •Viola Instruction •Upright Bass Instruction •Cello Instruction •Violin Instruction •Guitar Instruction •Jazz Guitar Instruction •Jazz Bass Instruction •Jazz Piano Instruction

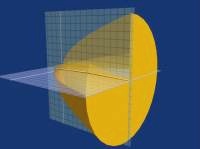
Topic - • Calculus VolsOfRevolution animation An animation of an arc on a grid where the arc is spun (lathed) on its X axis into a solid "bullet" shaped object. Then circular slices are highlighted, and one of them is then pulled from the object and spun around to show its shape. This introduces the topic of volumes of revolution. Vol_Using_Shells animation An animation of a parabola on a grid which is spun (lathed) on its Y axis to produce a "bundt cake" shaped half-donut. From this solid are highlighted rings, and one of the rings is pulled from the solid, opened up into a flat strip and spun around to show its shape. This introduces the topic of volume using the Shell method. 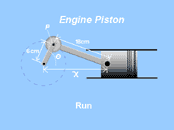Piston Animation This animation demonstrates a related rate application over time using a piston. 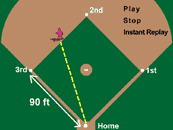BaseRunner Animation This animations depicts a rate of change topic using the runner's position relative to the home plate as he runs to third base. 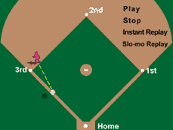BaseRunner_and_ball animation This animations depicts a rate of change topic involving a baseball player trying to throw a runner out at 3rd base. 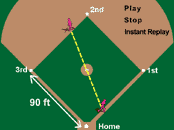BaseRunnerHome_and_2nd animation This animations depicts a rate of change topic involving the distance between two base runners. Cylinder_In_a_Sphere animation An animation of a blue wireframe globe spinning in place. Inside is a semi-transparent cylinder that expands and shrinks from a tall slim cylinder to a large diameter but thin slice of a cylinder and back again, showing all the possible variations of size and volume of a cylinder within a given sphere (a Max/Min problem). Cylinder_in_Sphere.jpg and Cylinder_in_Sphere_with_Labels.jpg (used in conjunction with the adjacent "Cylinder in a Sphere" animation) Silos animation An animation showing different views of four silos of different heights and diameters, visualizing how the various parameters effect the size and volume of the dome-shaped top. This is used to introduce a problem involving calculating the most cost-effective construction of a silo to hold a given volume of grain. The silo's domed top cannot be used to store grain and its cost of construction per volume measurement is greater than the cylindrical portion, thus creating the need to get the most cylindrical volume vs. dome volume to reduce construction cost for a given storage volume. (a Max/Min problem) 4_Silos_Front_View.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: 4_Silos_High_View.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: 4_Silos_Oblique_View.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_10x2.5.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_7.5x4.4.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_5x10.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_2.5x40.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_Transparent_ with_Labels.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: Silo_Transparent_no_Labels.jpg One of several still images from the "Silos" animation, showing various views of four silos, making it easier to visually compare the relative shapes and sizes: 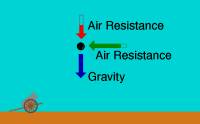CannonTrajectory_anim.gif An animation showing the forces on a projectile at different points in the flight path. Used for Calculus in solving differential equations and also for Euler’s Method. 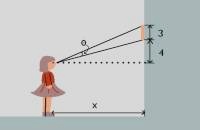Picture4 animation An animation - girl viewing a painting on the wall. Painting is 3' high, the bottom edge of it hangs 4' above the girl’s eyelevel. Find distance X from the wall where the girls viewing angle is best. 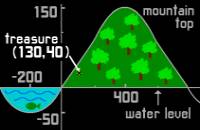TreasureDig animation An animation - a pirate buries his treasure in the side of a mountian that is an island. Picturing the island as a parabola on a grid, calculate whether the shortest route to dig to the treasure is a vertical or horizontal tunnel. Skater_anim.gif This animation shows an overhead view of an ice skater skating in an ellipse, which is superimposed on a coordinate plane. When the skater falls down, she slides off at a tangent to the ellipse (related rates problem). 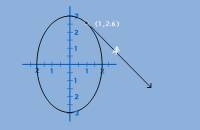Tartown_anim.gif In this animation two friends are talking on cell phones, each traveling in a car, one headed into Tartown, and one headed out of Tartown on highways that are at right angles to each other. From this overhead view, calculate the rate at which their distance from each other is changing (related rates problem). 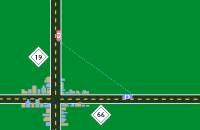Balloon_anim.gif An animation showing a hot air balloon going up vertically at 90 degrees. Balloon_70degrees_anim.gif An animation showing a hot air balloon going up vertically, but at a 70 degree angle to the ground. 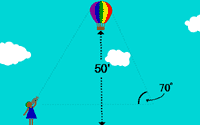BoatPull_anim.gif An animation. A man on a pier uses a rope to pull his rowboat closer to the pier. The rate of the boat’s approach changes with distance to the pier (related rates problem). 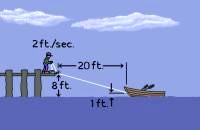Plane-n-Camera_anim.gif An animation showing a girl watching an approaching airplane through her video camera. The angle changes as the plane comes closer. (related rates problem) 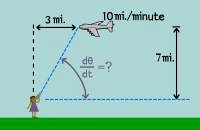RugbyField_anim.gif An animation. A player wants to find the optimum angle from the sideline to kick the ball into the goal so he has the widest possible target.

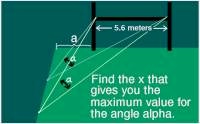Back to TOP - Menu < Previous Next >